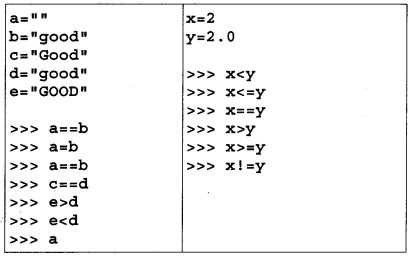
You can learn about Operators in Python Programs with Outputs helped you to understand the language better.
Python Programming – Relational/Conditional Operators
Relational Operators are used to comparing values. They are used to test the relation between two val¬ues and then return a boolean value either True or False. All Python relational operators are binary operators and hence, require two operands. A rela¬tional expression is made up of two arithmetic expressions connected by a relational operator. Comparison operators produce a Boolean result (type bool, either True or False). When a Boolean expression is evaluated, it produces a value of either true (the condition holds) or false (it does not hold). Conditions may compare either numbers or strings. If you compare strings, you get results based on alphabetical order.
- Python Programming – Operators
- Python Programming – Expressions
- Quick Tip: Using Python’s Comparison Operators | Chaining Comparison Operators in Python
|
Operator |
Symbol | Form |
Result |
| greater than | > | a > b | True if a is greater than b; else False |
| less than | < | a < b | True if a is less than b; else False |
| greater than or equal to | >= | a >=b | True if a is greater than or equal to b; else False |
| less than or equal to | <= | a <= b | True if a is less than or equal to b; else False |
| equal to | == | a == b | True if a is equal to b; else False |
| not equal to | != | a != b | True if a is not equal to b; else False |
For example, “apple” < “orange” is true, because “apple” is alphabetically less than “orange”. While comparing strings, the ordering is lexico-graphic (as in a dictionary). Basically, this means that strings are put in alphabetic order according to the underlying ASCII (American Standard Code for Information Interchange) codes. Lexicographical ordering is implemented using the corresponding ordinal value. So, all upper-case letters are considered lesser than lower case letters (For example, ‘A’ is less than ‘a’ because the ASCII value of ‘A’ (65) is lesser than ‘a'(97)).
The list of relational operators is given in Table 4.1
- You can check the ordinal value using ord(<cha- racter>), for example, ordC’A”) is 65.
For example,
>>> 5 < 8
True
>>> 5 < 3
False
>>> 5 < 7 < 10
True
>>> “Apple” < “Mango”
True
>>> “Orange” < “Mango”
False
>>> 7 > 3
True
>>> 5 <= 8
True
>>> 7 <= 5
False
>>> 5 != 6
True
>>> 4 != 4
False
>>> 5==5
True
>>> 4==5
False
>>> ‘Good’ == ‘Good’
True
>>> ‘Good’ == ‘Very Good’
False
>» ‘a’ == ‘A’
False
>>> ‘a’ > ‘A’
True
# because ordinal value of ‘a’ is 97 and ‘A’ is 65
>>> ‘a’ < ‘A’
False
>>> ‘python’ == ‘Python’
False ‘
>>> ‘Python’ == ‘Python’
True
>>> ‘Cat’ == ‘ Cat’
False
# because space is in the beginning, and ordinal value of space is 32.
>>> ‘Cat’ == ‘Cat’
True
# remove space before Cat, now the strings are equal
>>> ord(‘P’)
80
>>> ord(‘p’)
112
>>> ‘P'<‘p’
True
# ‘P’ is less than ‘p’ because ASCII value of ‘P’ (80) is lesser than ‘p'(112))
All the relational operators have lower precedence than the arithmetic operators. For example, the expression:
a + b*c<d/f
is evaluated as if it had been written as follows:
( a + (b * c )) < (d / f)
Example 2.
Consider the following declarations:
j = 0
m = 1
n = -1;
x = 2.5
y = 0.0
Evaluate the following expressions:
(a) j > m
(b) m / n < x
(c) j <= m >= n
(d) -x + j == y > n >= m
Solution:
(a) j > m is not true because the value of j = 0 and value of m = 1. Hence, the result is False.
(b) The expression m / n < x is equivalent to (m / n) < x because the precedence of / is higher than that of <. Substituting the values of the variables, you get the result as True.
(c) The expression j <= m >= n is equivalent to ((j <= m) >= n). Substituting the values of the vari-ables, you get the result as True.
(d) The expression -x +j == y > n >= m is equivalent to ((-x) +j ) == ((y > n) >= m). Substituting the values of the variables you get the result as False.
Let’s Try
Assign the given values to variable and write the output of the following relational operations: