Python Programming – Python Sets
As we have learned in mathematics about sets, the Python language also provides a new data type called set to handle all set operations. A set is an unordered collection of elements. There is no duplicity in the set and alike tuple, the set is immutable (can not alter). A set can contain a heterogeneous type of data. Since the set is an immutable data type, therefore, list or dictionary can not be set members. As mentioned earlier in Chapter 2, the sets can be used to perform all mathematical set operations such as union, intersection, difference, etc. In the following sub-section, we will learn Python set in detail.
Creating a Set
A set is created by using the built-in Python function set(). All the elements of a set are placed inside the set function by enclosing within braces { } and separated by commas. The programming example to create a set in Python is given in Code 5.27.
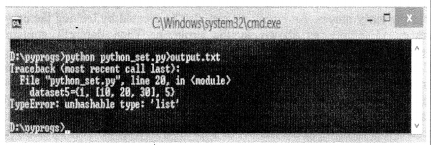
In this program, we explore all the methods of creating a set in Python. In the first part, the set is created with the named dataset by using the set() function. Secondly, a set is created without using the built-in set() function. The programmer must note that a set can also be created by putting its element into the curly braces. An empty set can also be created by leaving the curly braces {} empty as shown in the program. Then dataset4 contains heterogeneous kind of data, in which we see that dataset4 contains 3 elements, where the second element is a tuple.
Consequently, dataset5 is created with heterogeneous data set again. The dataset5 contains a list of its member. While executing this program, all the datasets from dataset through dataset4 provide the intended output. However, the printing of dataset5 results” into an error, as the list can not be a member of a set because Python sets are immutable entities and can not alter. Since lists and dictionaries are mutable, they can not be a member of a set. The output can be seen in the output section of this program:
- Python Programming – Standard Data Types
- Python Programming – Dictionaries
- Python Programming – Python Tuples
Code: 5.27. Illustration of creating a set in. Python.
| # creating a set in Python
# creating a set by using set function # creating a set without using set function #creating an empty set #creating heterogeneous set with tuple as element #creating heterogeneous set with list as element |
| Output
{1,2, 3, 4}
|
Changing/Adding Elements to a Set
As it is mentioned earlier that, sets are immutable, i.e., we cannot change the value of any element of a set. Moreover, sets are unordered therefore, indexing has no meaning in the context of sets. As a consequence of that, we cannot access the elements of a set by specific indexing and slicing operator.
Nevertheless, an element can be added to a set by using the add() method. If a user wishes to add more than one element, then this can be achieved by using the update() method of sets in Python. The programming illustration of using add() and update() methods is given in Code 5.28. In this program, we see that initially a dataset 1 is created with 4 elements {10, 20, 30, 40}. Then, a new element 35 is added to the set by using add() method of Python sets. Subsequently, 3 more elements together are added to the dataset by using the update() method.
It is to be noted that, more than one element can be added to the set using the update() method and in square brackets []. From the output of this program code, we see the intended results. Moreover, it is seen that the Python sets are unordered and the elements are displayed out of order despite their actual assignment while creating the set. This demonstrates that indexing has no relevance in sets. Thus, slicing and indexing operators cannot be used with sets.
Code: 5.28. Illustration of updating Python set.
| # updating a set in Python
dataset1={10, 20, 30, 40} datasetl ,update([5, 18,27]) |
| Output
{40, 10, 20, 30} |
Removing Elements from a Set
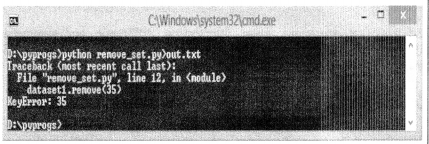
The Python language provides two methods discard() and remove( ) to remove elements from a set. Both of these functions perform the same task with the only difference that if the element to be deleted does not exist in the set then the remove() method raises an error. Whereas, the discard() method does not raise an error for the same case. The programming illustration for the same is given in Code 5.29. The program demonstrates that initially a dataset is created with 6 elements {10,20, 30,40,50,60}. Then, an element 30 is removed from the dataset by using the remove() method. Subsequently, an element 50 is deleted from dataset1 using the discard ( ) method. The updated dataset1 is printed after performing these two operations and we obtain the required output. Then, the discard ( ) method is used to remove 35 from the dataset1, although it does not exist in the set. It will not raise any error on the prompt. On the other hand, while using the remove ( ) method to eradicate 35 an error occurs as shown in the output section of this program.
Code: 5.29. Illustration of removing elements from a set.
| # removing an element from a set
datasetl={10,20, 30, 40, 50, 60} datasetl ,discard(50) datasetl ,discard(35) |
| Output
{40, 10, 50, 20, 60, 30}
|
There exist another method pop() to remove an element from a Python set. Since, the set is an unordered list of elements, the pop() method removes an element from the set randomly and the user does not need to provide the value of a specific element to be deleted as that for removes} and discards} methods. The Python language provides another method clear ( ) to remove all the elements of a set in one go. The programming illustration of pop() and clear() methods is given in Code 5.30. In this program, we see that by using the pop() method the element 40 has been removed from the set. The use of the clear ( ) method signifies the removal of all the elements of the set and an empty set is returned as an output.
Code: 5.30. Illustration of pop( ) and clear( ) methods.
| #illustration of pop( ) and clear( ) methods
dataset={10, 20, 30,40, 50, 60} dataset, clear}) |
| Output
{40, 10, 50, 20, 60, 30} |
Python Set Operations
The basic set operations union, intersection, difference, and the symmetric difference can be performed very efficiently over the Python sets. The description of each one of them is provided in the following sub-sections.
Set Union
The union of elements of x and y is the set of all elements of both sets. The duplicate elements are discarded in the union. The union of two sets x and y can be performed by using the operator (|) or by using the union() method. The programming illustration for the same is given in Code 5.31. It is apparent from the output that either by using the operator(|) or union() method, the result comes out to be the same.
Code: 5.31. Illustration of the union of sets in Python.
| #illustration of union operation on sets
x={10, 20,30} print(x|y) print(x.union(y)) |
| Output {50, 20, 40, 10, 60, 30} {50,20,40, 10, 60, 30} {50, 20, 40, 10, 60, 30} |
Set Intersection
The intersection of sets x and y refers to the common elements of both sets. The intersection of two sets can be performed either by using the (&) operator or the intersection( ) method of Python. The programming illustration for the intersection operation is given in Code 5.32. From the output section, we see that any of the three methods can be used to perform the intersection of two sets. The result is the common elements {20, 30} of both sets.
Code: 5.32. Illustration of intersection of sets in Python.
| #illustration of intersection operation on set
x={10,20, 30} print(x&y) print(x.intersection(y)) |
| Output
{20, 30} |
Set Difference
The difference of two sets x and y, (x-y) results in elements of x but not in y. Likewise, (y-x) refers to the elements of y but not in x. The intersection operation can be performed with the (-) operator or the difference() method of Python. The programming illustration of set difference is given in Code 5.33. It is apparent from the output that (x-y) and x.difference(y) results in elements of set x by excluding the elements of set y. Similarly, (y-x) and y.difference(x) results in elements of set y by excluding the elements of set x.
Code: 5.33. Illustration of difference of sets in Python.
| #illustration of difference operation on a set
x = { 10 , 20 , 30 } print (x-y) print(y-x) |
| Output
{10 , 20} |
Set Symmetric Difference
The symmetric difference of sets x and y refers to a set of elements contained in both x and y except those which are common among them. The symmetric difference is performed using the (A) operator or by using the symmetric_difference() Python method. The programming illustration of this operation is given in Code 5.34. It is apparent from the output of this program that any of the four operations written in the code can be used to perform symmetric differences on two sets x and y.
Code: 5.34. Illustration of symmetric difference.
| #illustration of symmetric difference operation on set
x={10,20,30} print(xAy) print(yAx) |
| Output
{40 , 10 , 20} |
python Set Method
The python language offers various methods to be used in conjunction with sets. Many of them, we have discussed in the previous sub-sections with their respective examples. The list of all the Python set methods is given in Table 5.8. with the description of each.
| Method | Description |
| add() | Adds multiple elements into a set |
| update() | Removes an element from the set. It does not raise error if element is not present in the set |
| discard() | Removes an element from the set. It raises error if element is not present in the set |
| remove() | Removes any random element from the set |
| Pop() | Removes any random element from the set |
| clear() | Removes all the elements of the set |
| copy() | Returns a copy of the set |
| union() | Returns the union of two sets |
| intersection() | Returns common elements in two sets |
| difference() | Returns the difference of two sets |
| symmetric_difference() | Returns symmetric difference of two sets |
| difference_update() | Removes all elements of another set from this set |
| intersection_update() | Performs the intersection operation of this set and another set and updates the current set |
| symmetric_difference_update() | Updates the set with symmetric distance of itself and another. |
| issubset() | Returns true if another set contains this set |
| issuperset() | Returns true if this set contains another set |
| isdisjoint() | Returns true if two sets have null intersection, i.e., returns true if two sets contain no common elements |
The in Operator
As we have learned in the previous sections the ‘in’ operator is used to test the membership of a particular element in the list and tuple. Similarly, the ‘in’ operator can be used to determine the membership of a set element also. The programming illustration for the same is given in Code 5.35. It is apparent from this code that as 10 is the member of set x. Therefore, the result of 10 in x comes out to be true. However, the result of 50 in y is false as 50 is not a member of set y.
Code: 5.35. Illustration of membership test using ‘in’ operator.
| #illustration of membership test of a set element
x={10, 20, 30} print(10 in x) |
| Output
True |
Alike lists and tuples the Python sets are also iterable. The ‘in’ operator is used with for loop to access all the elements of a set. The programming illustration for the same is given Code 5.36. This program illustrates that the set members can be accessed very efficiently by using for loop. The first set X is created, which contains numeric values.
Another set of cities are created, which contains name of three cities. Subsequently, a third set is created with the set function, which contains a string “Kolkata”. By using a for loop and in operator, all these three sets are accessed, which displays the elements of the set in arbitrary order for all three sets.
Code: 5.36. Illustration of accessing set elements using for loop.
| #illustration of accessing set elements using for loop
gx={10, 20, 30,40, 50} for n in gx: for city in cities: for c in set(“Kolkata”): |
| Output
40 a |
Python Set Functions
The Python language offers a set of functions to be used with sets. All the Python set functions are listed in Table 5.9. All these functions are quite simple and can be programmed very easily.
| Method | Description |
| all() | Returns true if all elements of the set are true |
| any() | Returns true if any element of the set is true. Returns false even if the set is empty |
| Len( ) | Returns the total number of elements in the set |
| max() | Returns the largest element in the set |
| min() | Returns the smallest element in the set |
| Sorted ( ) | Returns a sorted list of elements of the set |
| sum() | Returns the sum of all the elements of the set |
| Enumerate ( ) | Returns an enumerate object |
Frozen Sets
The Python language offers a new data type of sets called frozenset. As indicated by the name, the elements of a frozen set cannot be changed. As we know that tuples are immutable lists, similarly frozen sets are referred to as immutable sets. The frozenset() supports all the Python set methods except add(), remove(), and discard() because the elements of frozensets can not be altered. The programming illustration of frozenset is given in Code 5.37. it is apparent from the code that yset is a normal set, therefore a new element 12 is added to it by using the add method. On the other hand, the set is a frozenset. therefore, adding an element to it raises an AttributeError as shown in the output section of this program.
Code: 5.37. Illustration of frozenset ( ).
| #illustration of frozenset ( )
yset={40, 50, 60} xset=frozenset({10, 20, 30}) |
| Output{40, 50, 60, 12} Img |
Recommended Reading On: How to Access Element by Index in a Set | C