You can learn about Introduction to Programming Using Python Programs with Outputs helped you to understand the language better.
Introduction to Python Programming – The Basic Model Of Computation
The Basic Model Of Computation
A program is a set of instructions, written in a computer language, to perform a specific task. In an attempt to solve problems on a computer, one has to write a step-by-step solution using simple instructions for operations and thus, obtain the results. There would be a number of methods to solve a given problem, and therefore, solutions may differ from person to person. However, in all cases, the basic steps remain the same. These basic steps are as follows:
- Formulating the problem and deciding the data types to be inputted.
- Identifying the steps of computation that are necessary for getting the solution.
- Identifying decision points, i.e., under what circumstances a particular operation is to be performed and when not to be performed.
- Knowing the expected results and verifying with the actual values.
Procedure for Problem Solving
Problem-solving is the process involving basic sequential steps necessary to arrive at the solution of the given problem. It is a logical process of breaking down the problem into small parts which can be solved step-by¬step to obtain the result. This does not involve the computer.
Though every problem is unique in itself, a few basic steps for solving the problem are common. These steps should be understood thoroughly and practiced effectively. Using these steps, your problem-solving capability will improve with time. The six basic steps in solving a problem are as follows:
- Spend some time understanding the problem thoroughly. In this step, you are not required to use the computer. Instead, you should try to answer what is expected and how to obtain it. This means, try to solve the problem manually.
- Construct a list of variables that are needed to get the solution to the problem.
- Decide the layout for the output presentation.
- Select the programming technique which is best suited to solve the problem and, then only carry out the coding, using a suitable programming language.
- Test the program. Select test data so that each part of the program can be checked for correctness.
- Finally, use data validation steps to prevent the processing of wrongly entered data.
The above mentioned six steps are further elaborated in the following sections:
Step 1. Understanding the Problem
Read each statement given in the problem carefully so that you can answer the first question “What is expected by solving the problem?” Do not start drawing a flowchart or a decision table straight away. Instead, read each statement of the problem slowly and carefully by understanding the keywords. Use paper and pencil to solve the problem manually for some test data. Let us understand this point by solving the problem given in
Example 1.
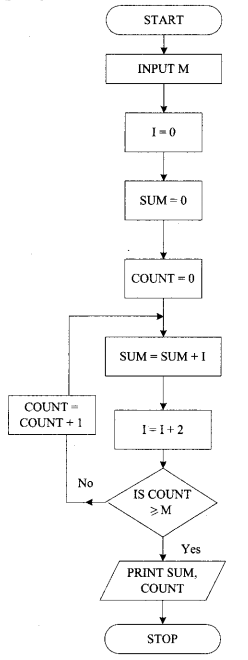
Accept a value M and find out the sum of the first M even integers.
Solution:
The solution to this problem requires you to draw a flowchart so that if you input 6 as the value of M (See Figure 1.1), the flowchart should give you the sum of the first 6 even integers. In the first step, you should be able to answer the following two questions:
“What are the first 6 even integers?”
These are 2, 4, 6, 8,10, and 12.
“What is their sum?”
Their sum is 42. Hence, the flowchart is to be framed in such a way that the sum of the first 6 even integers comes out to be 42.
- Introduction to Programming Using Python
- Introduction to Python Programming – Algorithms
- Introduction to Python Programming – Programming Languages
Step 2. Construction of the List of Variables
In this step, you should think in advance about the number of variables required and the name of the variables before drawing the flowchart. The names chosen for variables should be an aid to memory. For example, in the case of the problem stated in Step 1 given above, the variables may be I, SUM, and COUNT as given below.
- To generate even integers 2, 4, 6,…(I)
- To obtain the sum of even integers 2 + 4 + 6 + … (SUM)
- To count the number of even integers, i.e., count 1, 2, 3,… (COUNT)
Thus, it is clear that you need to use the above-mentioned three variables and one more variable “M” whose value will be input by the user of the program from the keyboard. Finally, the four variables are:
M To be inputted from the keyboard
I To generate even integers
COUNT A counter to keep a track of the number of even integers that have been summed up
SUM An accumulator that contains the current total of even integers
- A problem solver has to decide the various kinds of variables that take different values for finding the solution.
Step 3. Output Design
Often, the ‘output’ format is specified in the problem itself, but sometimes, it may not be so. If the output format is not specified, you must keep in mind that the output report should easily be understandable to a reader. The headings should not cause any doubt or confusion in the mind of the reader.
In the problem given in step 1 the output format could be as follows:
No. of Integers-6 Total Value-42 ‘
You should keep one point in mind. The programs and problem solutions are for other people (teachers, supervisors, contractors, etc.). They will appreciate you only if they can understand the results and analyze them. Hence, the output format should have the following characteristics:
a. Attractive
b. Easy-to-read
c. Self-explanatory
Step 4. Program Development
You should now draw a flowchart for the procedure that you have just made in Steps 1, 2, and 3. Standard symbols should be used for drawing the flowchart. If the problem is complex, you should divide it into several simpler parts. Then, draw a flowchart for each part separately and join them together using connectors.
The flowchart for the problem given in Example 1 is shown in Figure 1.1. Now, write the code in the pre-scribed high-level language to translate the flowchart into the program
Step 5. Testing the Program
You should give a dry run to the program developed in Step 4. This means giving some known values to the variables and checking the result by comparing them with manually calculated values. Test values are selected such that each part of the flowchart is tested, and consequently, the program is confirmed to be free from any logical errors.
Step 6. Validating the Data
It is quite likely that the user of your program may enter values that are not expected by the program. Such values should be rejected by the procedure created by you. This is known as validation of data. For example, in the problem stated in Step 1 given above, you may give the limit to the value of “M” and “M” should be an integer value. Such types of validation checks can be included in our program.
Problem Definition and use of Examples for Problem-Solving
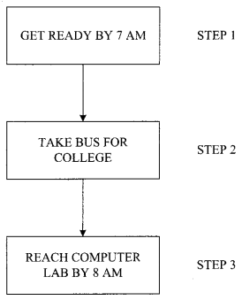
Let us take an example of a problem faced in day-to-day life. Suppose, you want to reach your computer laboratory by 8 AM. You would lay out a plan to get ready by 7 AM; then take a bus/rickshaw to reach the gate of your college. Then, climb up the stairs to arrive at the laboratory. You will note the time taken for each part. If due to some reason, you are unable to get ready by 7 AM, and you already know that it takes one hour to reach the college laboratory by bus/rickshaw, then you will take a faster means of transportation. You may take an auto-rikshaw or a taxi. Thus, a very simple problem of reaching the computer laboratory by 8 AM will need several steps to reach a solution. Each step is to be accurately defined/marked so that no guesswork is required.
You can thus represent the solution of this problem in three steps as shown in Figure 1.2. In Figure 1.2, Steps 1, 2, and 3 appear to be very simple. In actual practice, when you have to give instructions to a student who is going for the first time, it may not be so easy. For example, you have to define the word “READY” precisely so that he knows exactly what he has to do by 7 AM to get READY. Similarly, in Step 2, you may have to clearly specify the bus route number, the bus stop to board the bus, the place to get down from the bus, etc. You would also like to tell that the bus is not to be boarded if it is overcrowded. The word “over-crowded” needs to be exactly defined. Finally, Step 3 needs further elaboration about the floor and room number where the computer laboratory is located and how to reach there.
You can explain all this to a person who does not know anything about the computer laboratory, provided you know it correctly. In the same way, you can solve the problem on the computer, if you know exactly what it is and how to solve it manually. Let us solve a few problems using these methods.
Recommended Reading On: Computer MCQ Questions for Class 8 with Answers
